布尔代数上的位运算

 

           布尔代数是一个数学知识体系，它在0和1的二进制值上演化而来的。

           我们不需要去彻底的了解这个知识体系，但是里面定义了几种二进制的运算，却是我们在平时的编程过程当中也会遇到的。这四种运算分别是或、与、非和异或。下图展示了在布尔代数的知识体系中，对这四种运算的定义。

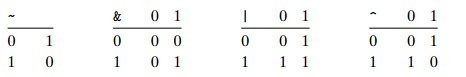
           从左至右依次是非、与、或以及异或。这个图阐述的是针对一位二进制的运算结果，我们可以将其扩大到N位二进制。比如两个二进制[a_w,a_w-1...a₁]和[b_w,b_w-1...b₁]，它们的四种运算则是对两者每一个相对应的位上做相应的运算。

           也就是说，倘若假设结果是[c_w,c_w-1...c₁]的话，那么对于任意c_i都满足 c_i = a_i (|,&,^) b_i，如果是对[a_w,a_w-1...a₁]进行非运算的话，那么c_i = ~a_i。

 

C语言上的位运算

 

           在C语言中，也支持位运算，而它的计算方式就是布尔代数中的位运算。位运算我们最常使用的是掩码的方式。比如我们知道一个整数x，如果我们想取得这个整数的最后一个字节的整数值的话，就可以采用位运算。就像下面这样。

#include 
     
      int main(){     unsigned int i = 0x12345678;     unsigned int j = 0xFF;     unsigned int k = i & j;     printf("%X\n",k);}
     

           最终我们希望得到的结果是78，也就是整数i的最后一个字节的值，我们使用掩码0xFF以及与运算过滤掉整数i的高位的三个字节。以下是结果。

    

C语言的逻辑运算

 

           C语言中的逻辑运算有||、&&和!，这比较容易与刚才的|，&和~搞混。逻辑运算比较特别，在这种运算的结果中认为所有非0的数值都是true，而为0的则为false。LZ在此写了一个小程序，我们来简单的看下二者的区别。

#include 
     
      int main(){      unsigned int x = 0x12345678;      unsigned int i = !x;      unsigned int j = ~x;      unsigned int m = !!x;      unsigned int n = ~~x;      printf("%u %u\n",i,j);      printf("%u %u\n",m,n);}
     

          从这个程序的结果可以很明显的看出!和~运算的区别，我们来直接看结果吧。

          结果很明显，左边是!x以及!!x的结果，只有0和1，而右边则是~x和~~x的结果。这里可以很明显的看出逻辑非与位的非运算的区别。前者只有0和1，而后者则是对每一位二进制值取反。

          除了结果上的区别之外，它们二者还有一个区别，就是逻辑运算倘若可以根据第一个表达式确定结果的话，那么将不会计算第二个表达式。举个简单的例子，假设有两个表达式a和b，对于a && b，倘若a为假，则不会计算b表达式的值。但是对于a & b则不同，无论a表达式的值为何，都要计算b表达式的值。

 

C语言的移位运算

 

          移位运算分为两种，左移和右移。对于一个二进制数[a_w,a_w-1,...a₁]来说，如果将它进行左移运算，则x << k = [a_w-k,a_w-k-1,...a₁,0,...0]。此时相当于最高的那k位都被丢弃了，在最右端补了k个0。而对于x >> k来说，也就是右移运算，与左移是类似的，只不过为了照顾有符号数，有时候需要在左端补最高位而不是0。而对于补0的情况，则称为逻辑右移，补最高位的则称为算术右移。

          也就是说，对于逻辑右移来说，x >> k = [0,...0,a_w,a_w-1,...a_k+1]，而对于算术右移来说，x >> k = [a_w,...a_w,a_w,a_w-1,...a_k+1]。

 

本章小结

 

          本章主要只是简单的介绍了下C语言中的位运算，下一章将会介绍一下整数的表示方式。